sometimes, I just think about odd science or technology. My wife has caught me multiple times using my kids' magna doodle, whiteboard, or chalkboard to work out some physics or stoichiometric equations … and that's just what she's noticed. :-)
I've put some such thought titles in the link-list. However, most of those were in the past, and it will take a while to re-create the thoughts here.
Some time ago, I tried coming up with my own water-drop/ripple simulation for making a small animated-gif background (akin to the moving backgrounds, like clouds, ocean breakers, etc, that are so popular as church lyric-projector backgrounds right now). Basically, I had a sinusoidish curve, decaying with radius and time; I simulated a dozen or so of these drips, usually centered off-picture, and added the curves; it made for some nice randomish moving water-surface. (Sorry, I cannot find where I put it for now.)
Anyway, I did a search, and found a YouTube video for a ripple using `z=(cos( 0.5sqrt(x^2+y^2)-6n)/(0.5(x^2+y^2)+1+2n))`, for `n={0...10}`. Based on a couple of quick spreadsheet graphs, it appears that `n` is the time element.
Note that this z-function has a similar response curve to sinc(t) = `sin(t)/t = s(t)`, but damps much more quickly. I think what I did in mine was base it on `s(t)*e^(-kt)`.
It looks like with the appropriate scaling on t, and choice of k, my since-with-exponential-decay could closely replicate the video's curve. I guess mine wasn't as poor of a choice as I thought at one time. Assuming that's what I really did.
I have just found an awesome way of embedding cross-browser math in a webpage: MathJax using AsciiMathML syntax. All you have to do is add a call to the MathJax JS library using their CDN call, and enclose a math expression in backticks(`), using the ASCIIMath syntax, which is easily summarized on one page; MathJax does the rest, to make the math show up cross-browser.
Example: hat(x)_(w)^2 ⇒ `hat(x)_(w)^2`.
My biggest complaint appears to be that MathJax uses the 1.4.7 version of AsciiMath, rather than 2.0; thus, among other things, it won't let me escape the back-ticks, so you cannot see them. View source.
Also, there might be a way to actually add graphs, too. Not with MathJax, but possibly with JSXGraph library (see this wiki. Exploring briefly, I think it will work... and I'm starting to really like the JSXGraph for interactive graphs as well.)
Update: yes, I have converted the graphs to JSXGraph! It's great!
So, as my daughter dropped her spoon at a meal yesterday, my son suggested we get her an anti-gravity spoon. I am a blessed man. :-)
I started thinking about the fact that people rarely think through the implications of suddenly defeating gravity's pull on a single object. Namely, that it's gravity that's providing the centripetal force to keep it moving with the planet.
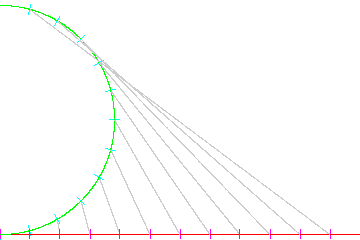
If my daughter has a spoon, and my son turns on it's antigrav device at the lower-left of my graph, then my daughter will continue following the round green path, moving 15° every hour, while the spoon takes off in the (originally) due-east straight-line red path, moving one tick every hour.
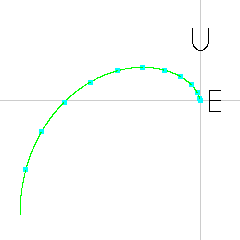
However, since my daughter will be moving in a curved-eastwards path, the spoon appears to be moving up-and-west, relative to my daughter: in the `(hat u, hat e)` coordinate system moving with my daughter and the earth, normalizing out the `r = R_E * cos(LAT)`, then `vec(up) = (\theta*sin(\theta\) + cos(\theta) - 1)*hat u`, and `vec(east) = (\theta*cos(\theta) - sin(\theta))*hat e`, where `\theta = \pi/(12hr) * time`. (It's graphed with east pointing right, and up pointing up.) After about 9 hours, the spoon would drop below my daughter's western horizon (as seen when the grey lines start intersecting the circle).
However, this is technically only the first-order approximation, where the antigravity device only cancels the earth's gravity, keeping the spoon affected by the sun's gravity. Without that, I'm not sure (yet), but I think the direction of the spoon will depend on the time of day and time of year. (And beyond that, we'd have to consider galactic and universal centers of gravity as well. But since we're not changing much with respect to those centers in the realm of watching a spoon fly away, I'll ignore those.) The solar analysis, including the tilt of the earth relative to it's orbital plane, will come later.
If you want the mathy-details, see my derivations.
(updates: , )
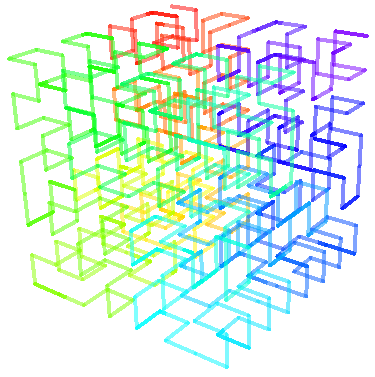
Robert Dickau's "Hilbert 3D curve,
iteration 3" (CC BY-SA)
I've been a fan of fractals since high school (and have even read Mandelbrot's Fractal Geometry of Nature). One of my favorite fractals is the Hilbert Curve. Many articles I've found try to explain how to generate a 3D version of the curve... but none to my satisfaction (meaning, they lost me at some point): mostly, because they seemed to be focused on an iterative loop to describe it, when it's simplest to describe in terms of a recursive algorithm. Studying Dickau's 3D image from the Hilbert Curve Wikipedia page, I was able to come up with a recursive 3D pseudo-turtle algorithm to draw it, and came up with a few other thoughts.
I hacked the following code up in Excel VBA, but then made the code more pseudo-code-ish.
LEVEL = 4
Call A(x, y, z)
function line(dir): draws a line in the direction of vector 'dir';
either go length=1 or length=2^(2*LEVEL) to stretch
Sub A(r, f, u)
If LEVEL < 1 Then Exit Sub
LEVEL = LEVEL - 1
l = -r
b = -f
d = -u
B(r, u, b)
line(u)
B(f, r, d)
line(r)
B(f, r, d)
line(d)
A(l, f, d)
line(f)
A(l, f, d)
line(u)
B(b, l, d)
line(l)
B(b, l, d)
line(d)
B(r, d, f)
LEVEL = LEVEL + 1
End Sub
Sub B(r, f, u)
If LEVEL < 1 Then Exit Sub
LEVEL = LEVEL - 1
l = -r
b = -f
d = -u
A(r, d, f)
line(d)
A(f, r, d)
line(r)
A(f, r, d)
line(u)
B(l, f, d)
line(f)
B(l, f, d)
line(d)
A(b, l, d)
line(l)
A(b, l, d)
line(u)
A(r, u, b)
LEVEL = LEVEL + 1
End Sub
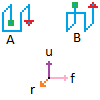A and B both traverse in the `hat f` direction (meaning the shape moves from START to FINISH = START + `hat f` ):
start at GREEN SQUARE, finish at RED ARROW. They both have two gaps: one in the `hat r` direction, and one
in the `hat f` direction. A follows the right-hand rule
by moving `hat u` first and then `hat r` to traverse the `hat f`
unit; B is the negative of A, so it follows the left-hand rule by moving -`hat u` (down) first, then continues
`hat r` and still traverses the `hat f` unit. (For A, if you curl your right hand, such that your palm and first
finger point up `hat u`, and your remaining fingers curl in the `hat r` direction, your thumb will point forward
in the `hat f` direction; the curl of your fingers matches the first two lines drawn in A, and your thumb
points the direction you will traverse. For B, use your left hand, with palm and first finger pointing
down -`hat u`, fingers curling to `hat r` direction, and thumb pointing forward `hat f`.) Whatever axis you pick
for `hat r`,`hat f`,`hat u`, as long as those axis follow the right hand rule ordering
(`hat(r) xx hat(f) = hat(u)`; eg, `hat x`,`hat y`,`hat z` where
`hat(x) xx hat(y) = hat(z)`, or `hat z`,`hat y`,-`hat x` because
`hat(z) xx hat(y) = -hat(x)`), you can always find a trio of axes such that `hat(r) xx hat(f) = hat(u)`.
Thus, while R.Dickau's algorithm of A → { A, A, …, A } (or the A → { B, B, … B} that seems to be in his Wolfram demo) fills the space, I think it violates the spirit of the 2d Hilbert curve, where "A → - B F + A F A + F B -" (ie, alternating B and A). I think a better combo for the 3d would be A → { B, A, A, B, B, A, A, B } with turns and forwards in appropriate locations; or A → { B, B, B, A, A, B, B, B }.
I'm considering changing my axis-order from "right, forward, up" to "up, right, forward", so that in the A-system, the first axis is the direction you draw, and you get a nice right-hand-rule curl to your fingers starting with the drawing direction, and ending with pointing ni the forward traversal direction. In this axis order, the B rule would have you draw first in the negative up direction, but the remaining drawing would be in the axial directions: thus, the drawing follows the left-hand rule, while the axes still follow the right-hand rule. I chose my current notation because filling the positive-x, positive-y, positive-z octant would be done with the natural notation A(x,y,z), but I think the effectiveness of the right-hand-rule for easily seeing the curl of the nodes will probably trump that "natural" notation.
I was taught that numbers that are divisible by 3 (or 9) will have the sum of their digits divisible by 3 (or 9) all the way down to one digit. But why do these numbers behave that way?
I haven't figured out the why, but have some ideas. I noticed that the divisible-by-3 rule applies not just for decimal-numbers, but for hexadecimal (base-16) numbers as well. However, the divisible-by-9 rule does not apply in hexadecimal. What's the difference? I've noticed that modulus is often important, especially for being one away from a "significant number" (power of two, prime), so maybe base as well. And digit d=3 has the property such that d*k+1=b, for bases b=10 and b=16. Testing other bases around those, I don't see the digits-divisible-by-3 applying for b=9,b=11,b=15, or b=17, where the d*k+1=b is not true. And for divide-by-9, d=9 has d*k+1=b for b=10, but not for b=16. I might be onto something. I also see that it doesn't seem to work for d>b.
I drive a Mazda RX-8, and ever since I heard about the RX-8
Hydrogen RE, I've wished it had made it into production in the United States. Every once in a while, I've googled to
see if there's anybody who converts RX-8's to dual-fuel hydrogen, but I've not found any yet.
It was this recent thought which prompted the electrolysis experiment, ostensibly with my kids.
And here's some raw notes to myself that I made when trying to figure out what mileage I might get (comparing combustion numbers on gasoline [octane] and hydrogen).
octane: 114.23g/mol 0.703g/cm3 255.68J/K/mol hydrogen: 2.0162g/mol 14.3kJ/K/kg .703g/cm^3 * 1cm^3/0.001L = 703g/L = 2661.14448g/gal 1 gal => 23.2963712 mol From GasolineVsHyFuelCell: 2 mol of octane combusted -> 10224kJ released -> 5112kJ/mol. 23.296 => 119 MJ 1 gallon of gasoline produces around 119MJ, and gets me 18miles 2 mol of hydrogen releases 486kJ, so 243kJ/mol To combust 119MJ of Hydrogen, at 119MJ / 243kJ/mol, need 490mol of H2. At 2.0162g/mol, Plug (0.703g/cm^3) * (1gal) / (114.23g/mol) * (5112kJ/mol) / (243kJ/mol) * (2.0162g/mol) into google search, which handles unit conversions for you 988.1g -- or about 1kg of H2 will produce as much energy as 1gal of gas
So, assuming it's purely energy that causes the rotation, I would use about 1kg of hydrogen per day
OTOH, assume it's really pressure (of PV=nRT fame) that causes the pushing. I'd need the specific heat to be able to convert the energy (assuming all heat) into a change in temperature... which would then change the pressure, causing the pushing.
But, I was able to find the DOE Hydrogen and Fuel Cells Program Record PDF, which says that 1kg of H2 is approximately 1 gallon-gasoline-equivalent on an energy content basis. Which means my calculations were reasonably accurate.
Some of my original links:
Ever since high school, when I first learned to derive the gravity of a sphere, I've wondered what gravity on a torus (donut) would be like. I learned quite quickly, then (and again recently) that the integration required for a donut goes beyond my ability. (Even showing the gravity inside a spherical shell requires integration tricks that I no longer remember, even after I recently read about how to do it.) So a few months back, I started a small computer program to do a brute-force summation of small pieces of the donut. I'm not sure I believe the numbers I got, so won't publish any of that. But I was able to find an article at io9, "What would the Earth be like if it was the shape of a donut", which brought out a lot I didn't think about. And MathPages has a full derivation of toroidal gravity, and makes me see why I couldn't do the calculus myself. :-)
So a radio host's silly quiz game had the failing caller "fall into a bottomless chasm" or some such phrasing. That got me thinking: it's bottomless, so there is nothing downwards from it; but if it's truly bottomless, you'd go through the center of the earth, at which point you could hit a "ceiling" at a rather high speed, since you'd be going upwards at this point. But if there were no ceiling, that would be like ultimate bungee!
Okay, it really wouldn't. Dr. Christopher Baird's blog has a detailed analysis, which points out (as I put it) "if the pressure doesn't kill you, the heat will". With atmosphere above you (on the way down), pressure will increase until you cannot breathe (20 atm of pressure at 0.15km), just like a submarine deep enough in the ocean. And it gets really, really hot the deeper you go (320 Kelvin at 1.1km will kill you of heat stroke; 1200 Kelvin by 200km will incinerate what's left).
But assuming you could protect yourself from the pressure and temperature (magic elevator cage), and assuming you liked bungee, that would be fun. Well, not bungee, yet, because the atmosphere, aside from crushing you, will decelerate you, too; you're stuck at terminal velocity (120mph or 200kph for a human-shaped elevator). So assuming you evacuated the pit, aligned the ends so they both punch through land rather than ocean, and could withstand the temperature, that would be a super-speed bungee.
Back in May 2014, I made a spreadsheet to make nice potential energy graphs:
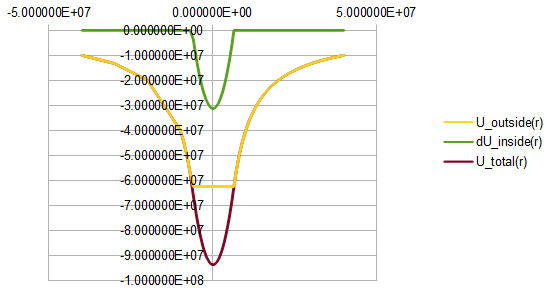
F(r) = -G M m / r^2
U = INTEG{INF to r}[ F(r) dr ]
r >e; Re
M(r>Re) = Me
F(r>Re) = -G Me m / r^2
U(r>e;Re) = -G Me m / |r|
r <e; Re
M(r<Re) = rho * (4/3) * pi * r^3
F(r<Re) = -G M(r) m / r^2
U(r<Re) = U(r=Re) - G m rho * (4/3) * pi * (Re^2 - r^2)/2
Then, find U(r=Re) and U(r=0): the delta will be the kinetic energy gain at the center of the earth. With K=1/2*m*v^2, I find that at the center, going about 8km/sec (almost 18000mph)!
Also, my old physics book (Halliday & Resnick (2nd ed), pg251) showed the calculation for how long it takes to do the round trip: because inside the uniform-density sphere approximation of the earth, force is directly proportional to distance from the center [F(inside)=-kx], then simple harmonic motion applies, and the period can be easily calculated at 84min, so you'd make the round trip in under 1.5hours.
But, once again, your radio host would have to be rather accomodating, especially if you want him to let you out of the elevator cage at the end of the trip. :-)
(GSU's HyperPhysics also shows the period calculation. And Wikipedia:Gravity_train brings up some of the results and issues involved.)